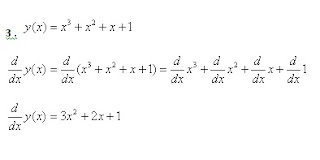miércoles, 6 de octubre de 2010
martes, 5 de octubre de 2010
viernes, 27 de agosto de 2010
jueves, 26 de agosto de 2010
VIDEO BUENO
http://www.youtube.com/watch?v=PwBdwnc621g
http://www.youtube.com/watch?v=yAB1Z5F0imI&feature=PlayList&p=322657BB25201A65&playnext=1&index=1
PROFEE. VI ESTE VIDEO PARA SABER HACER EJERCICIOS DE LIMITES EN GEOGEBRA PERO NO ENTIENDO .
http://www.youtube.com/watch?v=SzhavBH7zq8
http://www.youtube.com/watch?v=yAB1Z5F0imI&feature=PlayList&p=322657BB25201A65&playnext=1&index=1
PROFEE. VI ESTE VIDEO PARA SABER HACER EJERCICIOS DE LIMITES EN GEOGEBRA PERO NO ENTIENDO .
http://www.youtube.com/watch?v=SzhavBH7zq8
lunes, 16 de agosto de 2010
Definicion de Limites
Concepto que describe la tendencia de una sucesion o una funcion, a medida que los parametros de esa sucesion o funcion se acercan a determinado valor.
LEYES DE LIMITES
Progresiones
Profresion aritmetica => an= a1+(n-1)d
2,4,6,8,10 => la diferencia es constante
Progresion Geometrica
1,3,9,27 => la diferencia no es constante
Razon = an/an-1 = # x el anterior 3/1=3 9/3=3 27/9 = 3
Se halla la constante
Razon : diferencia constante de la progresion geometrica
. Las diferencias siempre son positivas
a20=2+(19)2
a20=2+19.2
a20=40
a21=2+(21-1)2
a21=42
Hallar en progresion aritmetica : 1,5,9,3,17
a15 = an= a1+(n1-11)d
a15=1+(15-1)4
=1+(14)4
1+14.4
=57
Hallar en progresion geometrica : 2,-6,18, -54
an/an(-1) = -6/2= -3 18/-6 = -3
an = a1 r *n-1
a15= 2.-3 *15-1
a15=2.-3*14
a15= 9,565.938
Hallar el quinceavo termino , empezando en 1 y va de 3 en 3
1,4,7,10,13,16,19 aritmetica, creciente , infinita
a15=
15= 1+(15-1)3
15=1+(14)3
15=43
2,4,6,8,10 => la diferencia es constante
Progresion Geometrica
1,3,9,27 => la diferencia no es constante
Razon = an/an-1 = # x el anterior 3/1=3 9/3=3 27/9 = 3
Se halla la constante
Razon : diferencia constante de la progresion geometrica
. Las diferencias siempre son positivas
a20=2+(19)2
a20=2+19.2
a20=40
a21=2+(21-1)2
a21=42
Hallar en progresion aritmetica : 1,5,9,3,17
a15 = an= a1+(n1-11)d
a15=1+(15-1)4
=1+(14)4
1+14.4
=57
Hallar en progresion geometrica : 2,-6,18, -54
an/an(-1) = -6/2= -3 18/-6 = -3
an = a1 r *n-1
a15= 2.-3 *15-1
a15=2.-3*14
a15= 9,565.938
Hallar el quinceavo termino , empezando en 1 y va de 3 en 3
1,4,7,10,13,16,19 aritmetica, creciente , infinita
a15=
15= 1+(15-1)3
15=1+(14)3
15=43
Limites y Sucesiones
miércoles, 2 de junio de 2010
CIRCUNFERENCIA
Una circunferencia es un conjunto de puntos del plano,distantes de otro fijo llamado centro; esta distancia se denomina radio. Sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.
PARTES DE LA CIRCUNFERENCIA
Centro: el punto interior equidistante de todos los puntos de la circunferencia.
Radio: el segmento que une el centro con un punto de la circunferencia;
Diámetro,o cuerda mayor, el mayor segmento que une dos puntos de la circunferencia, y lógicamente, pasa por el centro.
Cuerda, el segmento que une dos puntos de la circunferencia; las cuerdas de longitud máxima son los diámetros.
Recta secante, la que corta a la circunferencia en dos puntos.
Recta tangente, la que toca a la circunferencia en un sólo punto.
Punto de tangencia, el de contacto de la tangente con la circunferencia.
Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diametro.



PARTES DE LA CIRCUNFERENCIA
Centro: el punto interior equidistante de todos los puntos de la circunferencia.
Radio: el segmento que une el centro con un punto de la circunferencia;
Diámetro,o cuerda mayor, el mayor segmento que une dos puntos de la circunferencia, y lógicamente, pasa por el centro.
Cuerda, el segmento que une dos puntos de la circunferencia; las cuerdas de longitud máxima son los diámetros.
Recta secante, la que corta a la circunferencia en dos puntos.
Recta tangente, la que toca a la circunferencia en un sólo punto.
Punto de tangencia, el de contacto de la tangente con la circunferencia.
Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diametro.



martes, 1 de junio de 2010
Dificultad
Profe, aunque asisti varias veces a estudiar con ud y la mayoria lo tenian ocupado , yo tambien busque ayuda por otros lados , como compañeras del salon que les va muy bien en el tema , por ejemplo valeria, anita, andrea , alejandra cruz tambien me llego a explicar , le pregunte a una profesora de por mi casa , miraba videos en youtube o ejercicios que ud mismo nos mandaba al correo , leia esos conceptos.
Los ejercicios con los que estudio los hago bien y siento que entiendo, pero en el momento de la evaluacion no logro nada.
Yo pienso que es que yo no pienso mas alla, es decir, usted me da el ejercicio para pensar por que lado lo resuelvo , y yo me estanco.
Pero bueno, tratare de cambiar eso .
Los ejercicios con los que estudio los hago bien y siento que entiendo, pero en el momento de la evaluacion no logro nada.
Yo pienso que es que yo no pienso mas alla, es decir, usted me da el ejercicio para pensar por que lado lo resuelvo , y yo me estanco.
Pero bueno, tratare de cambiar eso .
HALLAR LA ECUACION CON EL VERTICE
lunes, 17 de mayo de 2010
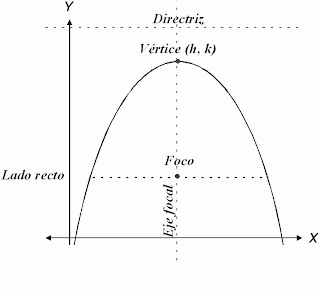
Foco y Directriz
Caracteristicas de la parabola
*Cuando todos sus valores son =1 , la parabola se divide un lado en el cuadrante I y III.
*Cuando la a es cero , la parabola abre hacia arriba y no corta el eje X.
*Cuando la a es positiva, la parabola queda en el cuadrante I y III y corta al eje X .
*Cuando la a es negativa queda en el cuadrante II y IV, y esta corta una ves al eje X.
*Cuando la b es =1 , la parabola corta el eje X en el punto (-1,0) y al eje y (0,1)
*Cuando se necesita la pendiente de la linea tangente , se realiza teniendo un punto y la funcion.
SECANTE : es una linea que intersecta dos puntos.
TANGENTE: es una linea que intersecta un punto.
IMAGEN: cuando el doy valores a X para a veriguar los puntos de la parabola; la Y se llama imagen .
*Si nos dan un punto y el vertice, se puede hallar la ecuacion.
*Cuando la a es cero , la parabola abre hacia arriba y no corta el eje X.
*Cuando la a es positiva, la parabola queda en el cuadrante I y III y corta al eje X .
*Cuando la a es negativa queda en el cuadrante II y IV, y esta corta una ves al eje X.
*Cuando la b es =1 , la parabola corta el eje X en el punto (-1,0) y al eje y (0,1)
*Cuando se necesita la pendiente de la linea tangente , se realiza teniendo un punto y la funcion.
SECANTE : es una linea que intersecta dos puntos.
TANGENTE: es una linea que intersecta un punto.
IMAGEN: cuando el doy valores a X para a veriguar los puntos de la parabola; la Y se llama imagen .
*Si nos dan un punto y el vertice, se puede hallar la ecuacion.
domingo, 11 de abril de 2010
SEGUNDO PERIODO
FUNCION CUADRATICA
ecuacion : ax(alados)+bx+c -----> representa una parabola
Si la a es negativa, la parabola esta abierta hacia abajo.
Si el valor de la a es cero , es una linea recta.
La b es el movimiento en el eje x .
Si la b es cero , coincide con el corte con el eje y .
La c es el movimiento de la parabola en el eje y.
PARTES DE LA PARABOLA

FOCO : es el centro de la parabaola.
VERTICE : punto medio entre el foco y la directriz.
SI la parabola va hacia arriba es el punto maximo , y si abre hacia abajo es el punto minimo.
SIGNIFICADO DE LA ECUACION CUADRATICA
Si la parabola corta el eje x en dos partes significa que la ecuacion tiene dos soluciones.
Si la parabola toca solo con un punto el eje x, tiene 1 solucion.
Cuando se halla el discriminante , estamos habllando los puntos de corte con el eje x.
Si el discriminante es negativo, no tiene solucion.
Si el discriminante NO tiene solucion NO toda el eje x .

ecuacion : ax(alados)+bx+c -----> representa una parabola
Si la a es negativa, la parabola esta abierta hacia abajo.
Si el valor de la a es cero , es una linea recta.
La b es el movimiento en el eje x .
Si la b es cero , coincide con el corte con el eje y .
La c es el movimiento de la parabola en el eje y.
PARTES DE LA PARABOLA

FOCO : es el centro de la parabaola.
VERTICE : punto medio entre el foco y la directriz.
SI la parabola va hacia arriba es el punto maximo , y si abre hacia abajo es el punto minimo.
SIGNIFICADO DE LA ECUACION CUADRATICA
Si la parabola corta el eje x en dos partes significa que la ecuacion tiene dos soluciones.
Si la parabola toca solo con un punto el eje x, tiene 1 solucion.
Cuando se halla el discriminante , estamos habllando los puntos de corte con el eje x.
Si el discriminante es negativo, no tiene solucion.
Si el discriminante NO tiene solucion NO toda el eje x .

martes, 16 de marzo de 2010
Suscribirse a:
Comentarios (Atom)